pKa and Electrical Properties of Amino Acids
In organic chemistry, pKa is a measure of the acidity or basicity of a compound. It represents the negative logarithm of the acid dissociation constant (Ka), which indicates the tendency of a molecule to donate or accept protons in a chemical reaction. Amino acids are unique organic molecules containing both an amino (-NH2) and a carboxyl (-COOH) functional group. Due to their dual nature, amino acids can exist in different protonation states, giving rise to multiple pKa values.
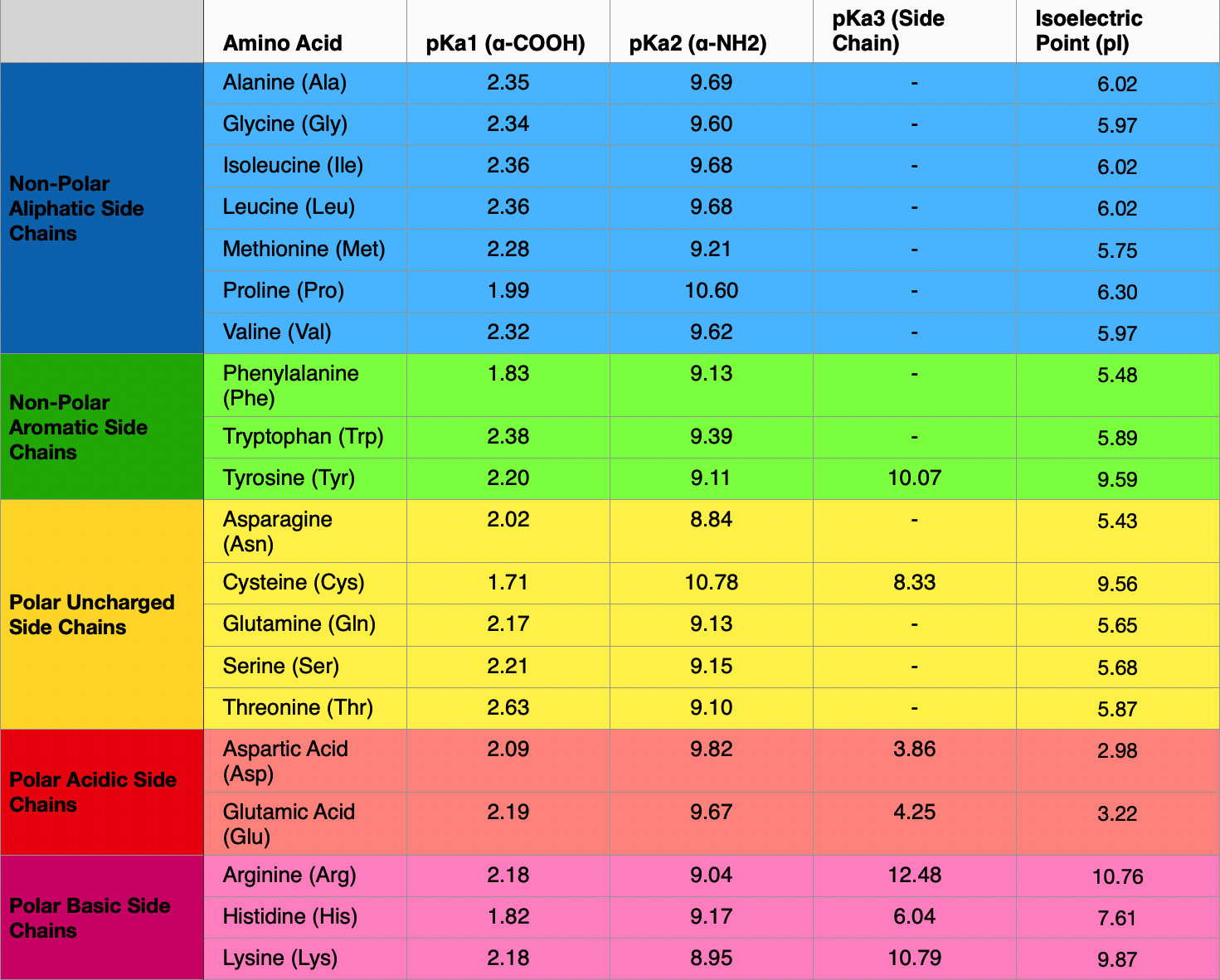
pKa of All 20 Amino Acids:
Zwitterions and Amino Acids:
A zwitterion, also known as a dipolar ion, is a molecule or ion that has both a positive and a negative charge within its structure, resulting in overall electrical neutrality. In the context of amino acids, zwitterions form due to the presence of both a protonated amino group (NH3+) and a deprotonated carboxyl group (COO-) at physiological pH (around 7.4). The amino group acts as a base and accepts a proton, while the carboxyl group acts as an acid and donates a proton. This unique property of amino acids allows them to exist as dipolar ions in an aqueous environment, rendering them excellent buffering agents and crucial components of proteins and enzymes.
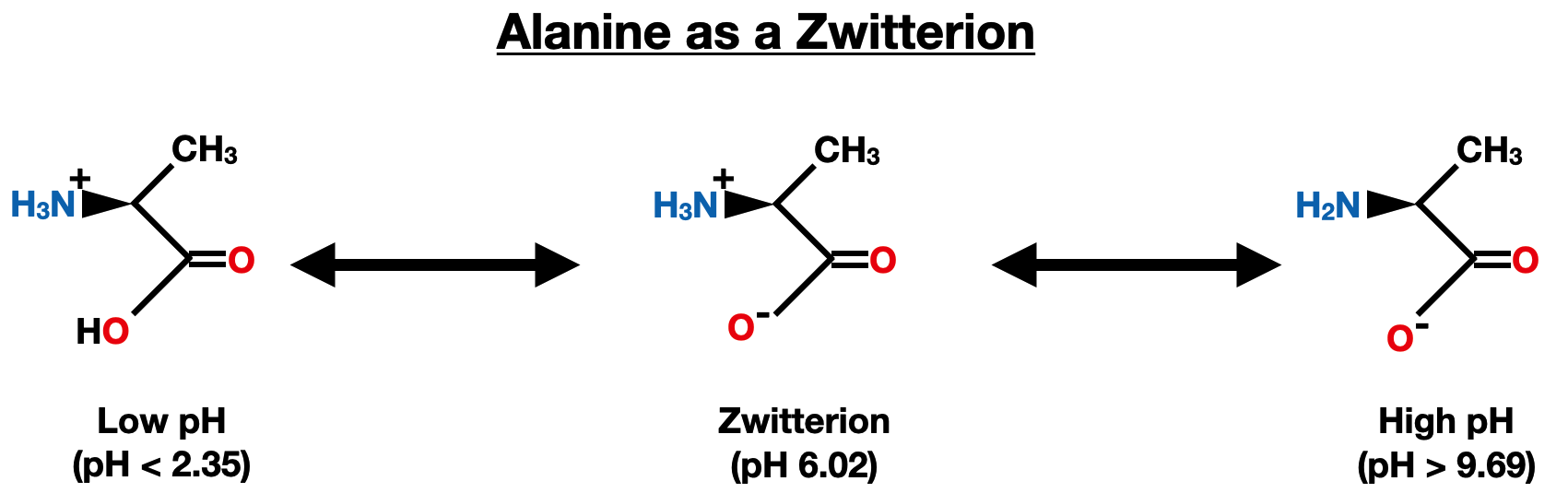
For example, consider alanine (Ala), which is a nonpolar, aliphatic amino acid. At low pH (acidic conditions), alanine predominantly exists in its protonated form (NH3+ and COOH) and specifically at pH below 2.35, it exclusively exists in this form. At high pH (basic conditions), it mainly exists in its deprotonated form (NH2 and COO-) and specifically at pH above 9.69, it exclusively exists in this form. At a pH of 6.02, both the amino group and the carboxyl group are simultaneously protonated and deprotonated, leading to the formation of the zwitterion (NH3+ and COO-), which has no net charge. This pH is known as the isoelectric point (pI) which is discussed below. At any pH in between 2.35 - 6.02 and 6.02 - 9.69, there is a mixture of the zwitterion and the protonated/deprotonated form.
Zwitterions are crucial for the overall structure and function of proteins as they play a vital role in stabilizing the three-dimensional structure through various interactions like hydrogen bonding and electrostatic interactions. Additionally, the existence of zwitterions is also relevant in the context of protein folding and enzyme catalysis. Their dual nature and ability to interact with both positively and negatively charged molecules make amino acids indispensable building blocks of life.
Isoelectric Points
The isoelectric point (pI) of an amino acid is the pH at which the molecule exists as 100% as a zwitterion, meaning it has no net electrical charge. At this specific pH, the amino acid's acidic and basic groups are protonated and deprotonated in such a way that the positive and negative charges effectively cancel out, resulting in a neutral overall charge. For amino acids with only one ionizable acidic group (carboxyl group) and one ionizable basic group (amino group), the pI can be calculated as the average of the two pKa values.
For example, let's consider alanine (Ala) again. Alanine has a carboxyl group (pKa ~ 2.34) and an amino group (pKa ~ 9.69). To determine the pI of alanine, we take the average of these two pKa values:
pI = (pKa of carboxyl group + pKa of amino group) / 2 pI = (2.35 + 9.69) / 2 ≈ 6.02
Therefore, the isoelectric point of alanine is approximately 6.02. At pH values lower than 6.02, alanine carries a net positive charge due to the protonation of its amino group. At pH values higher than 6.02, alanine carries a net negative charge due to the deprotonation of its carboxyl group. However, at the isoelectric point (pH ≈ 6.02), alanine exists predominantly as a zwitterion with no net charge.
If the amino acid has a side chain that also has a pKa (pKa 3 in the table above), the isoelectric point is determined by taking the average of the two closest pKa values. Lets examine aspartic acid and lysine.
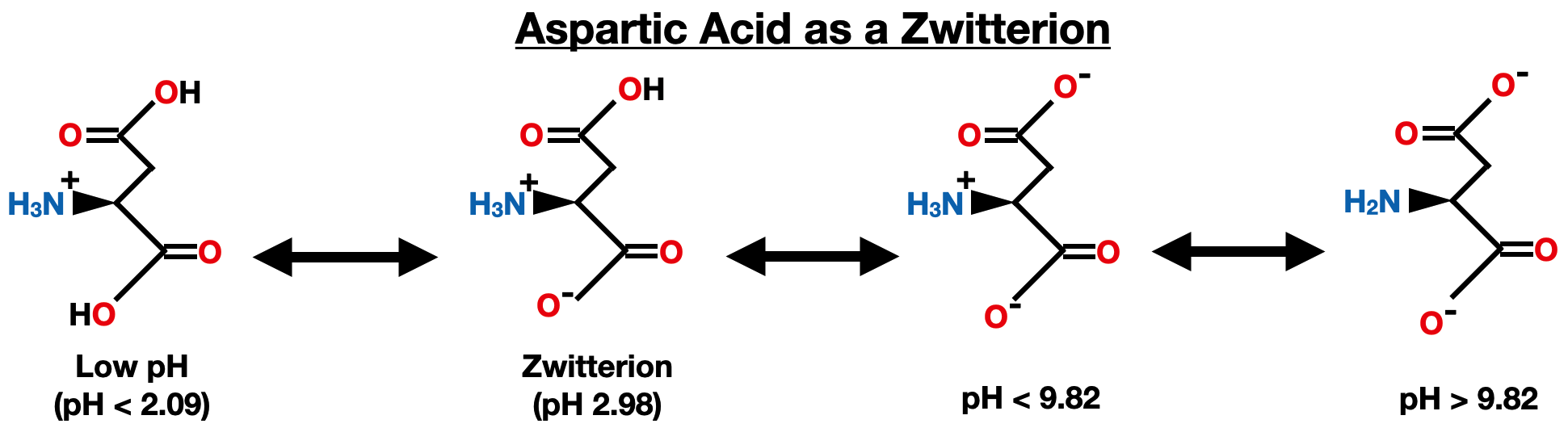
Aspartic acid has an acidic side chain with a pKa of 3.86 (pKa 3) and the carboxylic acid pKa is 2.09 (pKa 1): pI = (pKa of carboxyl group + pKa of side chain group) / 2 pI = (2.09 + 3.86) / 2 ≈ 2.98
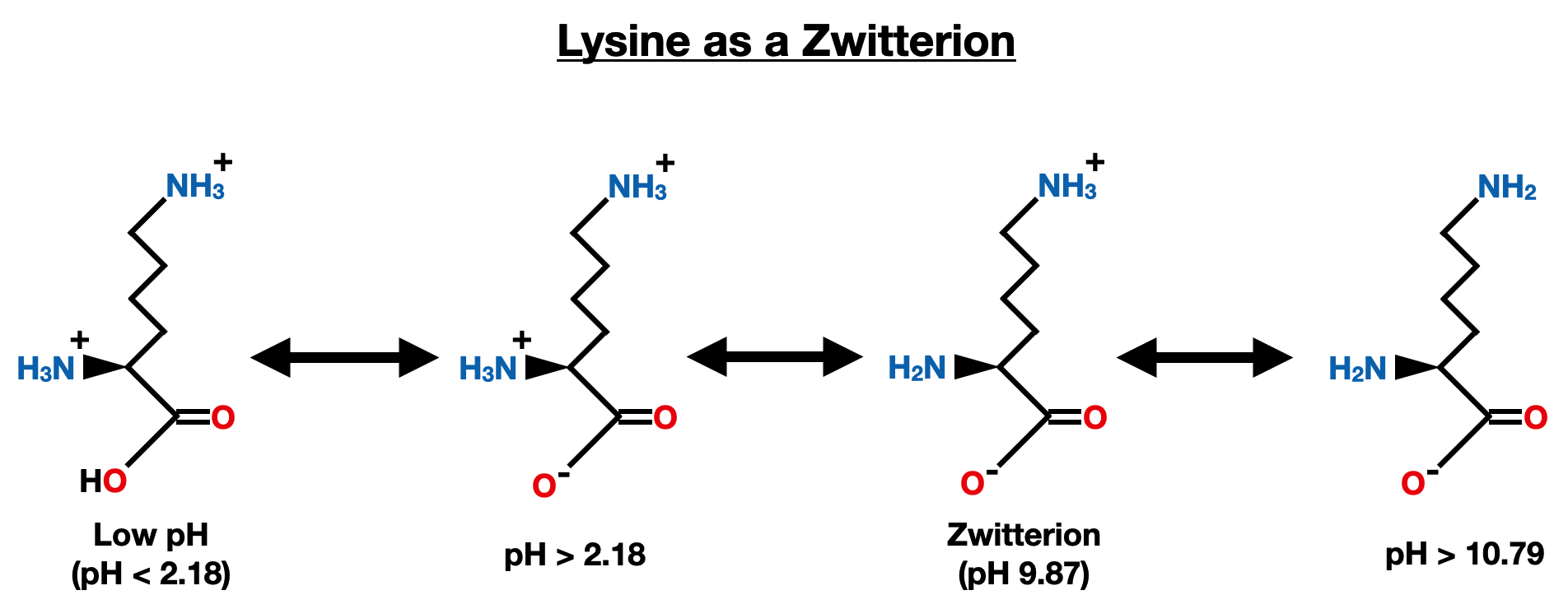
Lysine has a basic side chain with a pKa of 10.79 (pKa 3) and the amino pKa is 8.95 (pKa 2): pI = (pKa of amino group + pKa of side chain group) / 2 pI = (8.95 + 10.79) / 2 ≈ 9.87
The concept of the isoelectric point is critical in understanding protein behavior, especially during techniques like electrophoresis, where proteins can be separated based on their charges at different pH values. Moreover, knowing the pI of amino acids is essential in predicting the behavior of peptides and proteins in various biological contexts, such as enzyme catalysis, protein-protein interactions, and protein folding.
Summary
Understanding pKa, zwitterions, and isoelectric points in amino acids is critical in comprehending the behavior and properties of proteins and their functional groups. The multiple pKa values and the formation of zwitterions in amino acids give rise to the complex behavior of these molecules, which plays a significant role in protein folding, interactions, and enzymatic functions. The concept of pKa and its application to amino acids provide valuable insights into the underlying principles of biochemical reactions and the intricate balance of charges that govern biological systems.
Test Your Knowledge:
How do you calculate an isoelectric point?
When the pH is in between the pKa of the different functional groups, what does the molecule look like? Use Valine, Glutamic Acid, and Lysine as examples.